<ML논문> 클래스 불균형 문제 Cui et al. "Class-Balanced Loss Based on Effective Number of Samples" (CVPR 2019)

 

TL;DR

Class imbalance 문제를 해결하기 위해서 데이터셋 각 클래스의 유효 데이터 수를 정의하고 이를 활용한 re-weighting기반 Class Balance Loss 기법 제안.

 

 

무슨 문제를 풀고 있나?

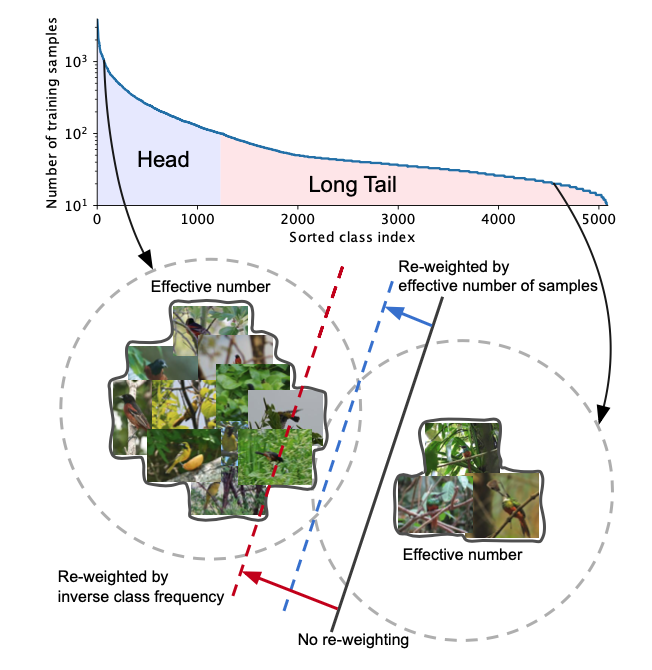
딥러닝 모델 학습에 사용되는 일반적인 데이터 셋 (예를들어 CIFAR-10, 100, ImageNet 등)이 클래스 라벨 분포가 균일한 것과 달리, 실제 상황에서는 모든 클래스의 데이터 수가 균일하게 수집되지 않는, Long Tail 현상이 발생한다. 여기서 Long Tail이라고함은, 각 학습 데이터 의 클래스 별 샘플 수에 대한 분포를 그렸을 때 아래 그림과 같이, 소수의 클래스에 대해서 데이터 샘플 수가 많은 데 반해 (Head) 다수의 클래스에서 기대치 이하의 샘플 수를 갖는 (Long Tail) 현상을 말한다. 말 그대로 클래스 샘플 수의 분포를 그렸을때 긴 꼬리를 가진다는 뜻이다.

 

요약하자면, 본 논문에서는 학습 데이터 셋 내의 클래스 불균형 문제 (Class Imbalance Problem) 를 다루고 있다.

 

그림 출처: Cui et al. Figure 1

 

기존 연구들은 이 문제를 어떻게 다루었나?

 

기존 연구들은 문제 해결 방식에 따라 크게 Re-sampling방식과 Cost-sensitive re-weighting 방식으로 나뉜다.

- Re-Sampling

Re-sampling방식은 말 그대로 실제 있는 데이터 수를 중복해서 sampling하는 방식이다. 예를 들어 데이터 수가 적은 클래스에 대해서 중복해서 더 샘플링을 하거나 (over-sampling) 샘플 수가 많은 클래스에 대해서 덜 샘플링 하거나 (under-sampling) 하는 형태이다. 이 경우 샘플 중복으로 인한 과적합 (overfitting)이 일어날 수 있고, over-sampling을 하는 경우에 상대적으로 학습 시간이 증가하는 이슈 역시 고려되어야한다. 이러한 한계점으로 인해 Re-sampling 방식보다는 Re-weighting방식이 좀 더 선호된다.

 

- Re-weighting

Re-weighting 방식은 클래스 별 샘플 수에 따라서 학습 시 손실 함수에 가중치를 주는 방식을 말한다. 예를 들어, 상대적으로 소수의 클래스에 대한 loss 값에 더 높은 가중치를 주는 형태이다. 상대적으로 간단하다는 장점으로 인해 이 방식이 많이 사용되었으나, large-scale 데이터 셋에 대해서는 이러한 단순한 방식이 잘 동작하지 않는 다는 사실이 확인되었다. 대신 "smoothed weight" 손실 함수에 대한 연구가 진행되었다. "smoothed" 버전의 경우에는 클래스 분포의 제곱근에 반비례하도록 weight를 준다.

 

 

이 논문에서는 이 문제를 어떻게 풀고 있나?

Conceptually,

본 논문에서는 Re-weighting기법에서 착안한 방법을 제안한다. 아래의 2개의 클래스를 예로 들어 설명해보면, 왼쪽은 Head에 해당하는 데이터 샘플이고 오른쪽은 Long Tail에 해당하는 데이터 샘플이라고 하자. 기존의 re-weighting 방법은 왼쪽 클래스 샘플의 수와 오른쪽 클래스 샘플의 수를 가지고 weighting을 수행했지만, 이 경우 검은색 실선으로 그려진 classifier 선이 빨간색으로 치우치게된다. 하지만 클래스 내의 모든 샘플들이 유효한 수를 구성하는 것은 아니라는 점을 상기해야한다. 예를 들어, 샘플들 간에 중복되는 정보를 가지고 있는 데이터가 있을 수도 있기 때문에 단순히 '샘플의 수'를 loss의 weight로 정하는 것은 문제가 될 수 있다. 따라서 본 논문에서는 각 클래스 별 '샘플의 유효 숫자 (effective number)'를 구하는 방법을 제안하고 있으며, 이렇게 구해진 유효 개수에 반비례하도록 loss를 re-weighting을 하는 경우 검은색 선으로 치우친 classifier를 우리가 원하는 파란색 선과 같이 조정할 수 있다.

 

그림 출처: Cui et al. Figure 1

유효 샘플 수 (Effective Number of Samples)

본 논문에서는 각 데이터 셋의 클래스 별 유효 샘플 수를 어떻게 구하는지를 제안하고있다. 이를 위해 논문에서는 유효 개수 (Effective Number) 를 다음과 가이 정의하고 있다.

 

Definition 1 (Effective Number).
The effective number of samples is the expecterd volume of samples.

 

샘플 크기의 기댓값을 샘플의 유효 개수로 정의하고있다.

 

기댓값을 정의하기 위해서 본 논문에서는 새로 샘플링한 데이터가 지금까지 관찰된 샘플과 겹칠 확률을 $p$, 겹치지 않을 확률을 $1-p$로 상정한다 (이 때, 문제를 단순화하기 위해서 일부만 겹치는 경우에 대해서는 고려하고 있지 않습니다) 이를 그림으로 그려보면 다음과 같다.

 

그림 출처: Cui et al. Figure 2

 

 

부연 설명

본 논문의 아이디어는 클래스의 데이터를 더 많이 사용할 때 marginal benefit이 줄어드는 정도를 측정하는 것이다. 예를 들어, 샘플의 수가 증가하면 새로 추가되는 샘플이 현재 존재하는 샘플과 겹칠 확률이 높아진다. (심플한 데이터 증강 - 회전, 크로핑 등 - 으로 확보된 데이터 역시 중복되는 데이터로 볼 수 있습니다.)

 

이제 샘플의 유효 개수 (expected number or expected volume)를 수학적으로 표현해볼 수 있다. 먼저 해당 클래스의 피쳐 공간에서 모든 가능한 데이터의 집합을 $\mathcal{S}$라고 하고, 이러한 집합 $S$의 크기를 $N$이라고 가정한다. 그리고 우리가 표현하고자하는 샘플의 유효 개수를 $E_n$으로 표기하겠습니다. 여기서 $n$은 샘플의 수를 의미한다.

 

그러면 샘플의 유효개수는 다음과 같이 표기할 수 있다.

 

 

Proposition 1 (Effective Number).
$E_n = (1-\beta^n)/(1-\beta)$, where $\beta = (N-1)/N$.

 

 

증명 설명

귀납법으로 이를 설명해보면 다음과 같습니다. 먼더 $E_1 = 1$을 만족하고 (overlap이 없기 때문에) 이는 $E_1 = (1-\beta^1)/(1-\beta)=1$을 만족합니다. 이제 과거에 샘플된 $n-1$개의 예제로부터 $n$번째 샘플을 샘플링했다고 가정해보겠습니다. 그러면 새로 샘플된 데이터가 이전의 샘플들과 overlap될 확률은 전체 집합$S$의 개수 $N$중 $E_{n-1}$일 확률, 즉 $p=E_{n-1}/N$을 만족합니다. 따라서 $n$개의 샘플에 대한 유효 개수의 기댓값은 $E_n = p \cdot E_{n-1} + (1-p)(E_{n-1} + 1) = 1 + \frac{N-1}{N}E_{n-1}$을 만족합니다. 귀납법에 의해서 $E_{n-1}  = (1-\beta^{n-1})/(1-\beta)$를 만족한다고 가정했을 때, $E_n = 1+\beta \frac{1-\beta^{n-1}}{1-\beta} = \frac{1-\beta+\beta-\beta^n}{1-\beta} = \frac{1-\beta^n}{1-\beta}$ 를 만족함을 확인할 수 있습니다.

 

Effective Number에 대한 추가적인 이해

그리고 위의 proposition으로부터 우리는 샘플의 유효 개수가 $n$에 대한 지수함수임을 확인할 수 있습니다. (참고로, $\beta$는 0에서 1 사이 $[0,1)$ 확률을 의미합니다) 그리고 참고로 $\beta$는 $n$이 증가함에따라 $E_n$이 얼마나 빨리 증가하는지를 결정한다고 볼 수 있습니다. 그러면 class를 표현할 수 있는 집합 $S$ 의 전체 크기 $N$은 어떻게 구할 수 있을까요? $E_n = (1-\beta^n)/(1-\beta)=\sum_{j=1}^{n} \beta^{j-1}$로부터 $N$은 다음의 극한으로 구할 수 있습니다. $N = \lim_{n\rightarrow \infty} \sum_{j=1}^{n} \beta^{j-1} = 1/(1-\beta)$. 이로부터 $\beta = 0$이면 $E_n=1$ 을 만족하고 $\beta$가 1에 가까워질수록 $E_n \rightarrow n$를 만족함을 알 수 있습니다.

 

 

Class-Balanced Loss

 

앞서 설명했듯이, 본 논문은 기존의 연구들 중 loss에 class별 re-weight를 주는 방법론들의 한계와 아이디어를 Effective Number라는 개념을 도입함으로써 개선하고 있다. 이 논문의 장점은 loss function에 agnostic 하다는 점이다. 실제로 본 논문에서는 Cross-Entropy Loss (Softmax, Sigmoid)와 Focal Loss에 대한 예제를 함께 제시하고있다.

 

입력 $\boldsymbol{x}$와 라벨 $y \in \{1, 2, \cdots, C$가 주어지고 $C$개의 클래스가 있다고 가정했을 때, 모델의 추정 class probability를 $\boldsymbol{p} = [p_1, p_2, \cdots , p_C]^T$ 로 주어진다고 가정한다. 이 때의 손식 함수를 $\mathcal{L}(\boldsymbol{p}, y)$를 표기한다.

 

그러면 클래스 $i$의 샘플 수를 $n_i$라고 했을 때, 앞의 Proposition에 의해서 해당 클래스의 effective number는 $E_{n_i} = (1-\beta_i^{n_i})(1-\beta_i)$를 만족하고 이 때 $\beta_i = (N_i - 1)/N_i$를 만족한다. 근데 문제는 $N_i$는 그 정의에 따르면 클래스의 가능한 모든 샘플 집합 $S_i$의 크기이기 때문에 구할 수 없다. 따라서, 실제 학습에서는 $N_i$가 오직 데이터셋에 의존적이고, 모든 클래스 $i$의 $N_i$가 다음과 같이 동일하다고 가정한다 $N_i = N, \beta_i = \beta = (N-1)/N$.

 

이렇게 구한 effective number를 사용하여 손실함수를 balancing 하기 위해서 논문에서는 "weighting factor $\alpha_i$"를 도입합니다. weigthing factor $\alpha_i$는 class $i$의 유효 샘플 수에 반비례하는 항이다: $\alpha_i \propto 1/E_{n_i}$. (앞의 Re-weighting 기존 연구 참고) 추가적으로, Weigting factor를 적용했을 때 스케일을 조절해주기 위해서 전체 클래스에 대해서 weighting factor들을  정규화해준다. ($\sum_{i=1}^{C} \alpha_i = C$)

 

이를 종합한 class-balanced (CB) loss는 다음과 같다.

 

• class $i$의 샘플 수를 $n_i$라고 하자
• $\beta \in [0,1)$일 때, class $i$의 weighting factor는 $(1-\beta)/(1-\beta^{n_i})$이다.
• 이 때의 CB loss는 다음과 같다: $CB(\boldsymbol{p}, y) = \frac{1}{E_{n_y}}\mathcal{L}(\boldsymbol{p},y) = \frac{1-\beta}{1-\beta^{n_y}}\mathcal{L}(\boldsymbol{p},y)$

참고로, $\beta = 0$이면 weighting을 주지 않는것과 같고, $\beta$ 값이 1에 가까워질수록 class frequency만으로 re-weighting하는 것과 유사한 효과를 나타낸다.

 

 

EX) Class-Balanced Softmax Cross-Entropy Loss

 

Softmax Cross-Entropy loss에 Class Balance (CB)를 적용해보자. 먼저, 모델로부터 주어진 각 클래스별 예측 결과를 $\boldsymbol{z} = [z_1, z_2, \cdots, z_C]^T$라고 하자. 그러면 softmax cross-entropy loss는 다음과 같이 주어진다:

 

$CE_{softmax}(\boldsymbol{z}, y) = - \log \Big( exp(z_y)/\sum_{j=1}^{C} exp(z_j) \Big)$

 

여기에 Class Balance를 적용시키면 다음과 같다. 라벨 $y$에 대응되는 클래스 학습 샘플 수가 $n_y$라고하면, CB loss는 다음과 같이 주어진다.

 

$CB_{softmax}(\boldsymbol{z}, y) = - (1-\beta)/(1-\beta^{n_y}) \cdot \log \Big( exp(z_y)/\sum_{j=1}^{C} exp(z_j) \Big)$

 

 

 

Code 들여다보기

(코드 출처: https://github.com/vandit15/Class-balanced-loss-pytorch/blob/master/class_balanced_loss.py)

def CB_loss(labels, logits, samples_per_cls, no_of_classes, loss_type, beta, gamma):
    """Compute the Class Balanced Loss between `logits` and the ground truth `labels`.

    Class Balanced Loss: ((1-beta)/(1-beta^n))*Loss(labels, logits)
    where Loss is one of the standard losses used for Neural Networks.

    Args:
      labels: A int tensor of size [batch].
      logits: A float tensor of size [batch, no_of_classes].
      samples_per_cls: A python list of size [no_of_classes].
      no_of_classes: total number of classes. int
      loss_type: string. One of "sigmoid", "focal", "softmax".
      beta: float. Hyperparameter for Class balanced loss.
      gamma: float. Hyperparameter for Focal loss.

    Returns:
      cb_loss: A float tensor representing class balanced loss
    """
    effective_num = 1.0 - np.power(beta, samples_per_cls)
    weights = (1.0 - beta) / np.array(effective_num)
    # normalization
    weights = weights / np.sum(weights) * no_of_classes

    labels_one_hot = F.one_hot(labels, no_of_classes).float()

    weights = torch.tensor(weights).float()
    weights = weights.unsqueeze(0)
    weights = weights.repeat(labels_one_hot.shape[0],1) * labels_one_hot
    weights = weights.sum(1)
    weights = weights.unsqueeze(1)
    weights = weights.repeat(1,no_of_classes)

    if loss_type == "focal":
        cb_loss = focal_loss(labels_one_hot, logits, weights, gamma)
    elif loss_type == "sigmoid":
        cb_loss = F.binary_cross_entropy_with_logits(input = logits,target = labels_one_hot, weights = weights)
    elif loss_type == "softmax":
        pred = logits.softmax(dim = 1)
        cb_loss = F.binary_cross_entropy(input = pred, target = labels_one_hot, weight = weights)
    return cb_loss

 

 

 

Reference

(Cui et al. 2019) Cui et al. "Class-Balanced Loss Based on Effective Number of Samples", CVPR 2019

 

 

 

 

 

 

내용에 대한 코멘트는

언제든지 환영입니다

끝 ◼︎