<ML논문> CVAE에 대하여 (feat. 누가 진짜 CVAE인가? 하나의 이름, 두 개의 기법)

 

---

<들어가기에 앞서>

본 글은 논문의 상세 내용을 다루는 포스팅은 아니에요.

다만, 두 개의 논문이 하나의 이름으로 불리고 있길래, '이에 대한 혼선을 정리하는 글을 써보자'하는 마음으로 글을 썼습니다.

물론 간략하게 각각의 논문 내용을 다루고 있기는 합니다만, 자세한 내용은 각 논문 내용을 설명하는 글을 참고해주세요.

 

감사합니다.

---

 

 

안녕하세요. 오늘은 개인적으로 흥미로웠던 현상에 대해 적어볼까 합니다.

 

이 본문을 읽고 계신 99.9 % 의 분들은 "CVAE"라는 키워드를 검색하셨을 것 같아요. 여러분이 이 글을 클릭하실 때 생각하신 CVAE는 어떤 녀석인가요? 질문이 이상하죠? 제가 오늘 이 글을 쓰기로 마음먹은 데는 이유가 있습니다. 제가 검색을 하다가 발견한 현상이 있는데, 바로 두 개의 (유관하지만 서로 다른) 논문이 Conditional Variational Auto-Encoder (CVAE)라는 하나의 이름으로 명명되고 있더라고요. 그래서 다음 주제로 글을 써보려고 합니다.

 

 

 

 

 

누가 진짜 CVAE인가?

(두둥)

 

 

 

 

 

 

CVAE라는 이름의 두 논문

 

 

본 글의 기획은 제가 CVAE 오픈 소스 코드를 검색하면 서부터입니다. 논문을 읽고 제가 이해한 내용을 검증하기 위해서 CVAE 코드를 검색하기 시작했는데, 검색하면 할수록 뭔가 이상하다는 생각이 들었어요. 제가 읽은 논문 내용과 맞지 않은 github 코드가 있거나, 혹은 제가 읽은 논문과 다른 내용의 설명들이 있더라고요. 그래서 알게 된 게, 사람들이 CVAE로 부르는 기법이 완전히 다른 두 논문의 내용이라는 사실이에요.

 

하나는, DP Kingma 아저씨 (?)의 (Kingma et al. "Semi-supervised Learning with Deep Generative Models", NIPS 2014)이고, 다른 하나는 이홍락 교수님 랩에서 나온 (Sohn et al. "Learning Structured Output Representation using Deep Conditional Generative Models" NIPS 2015)입니다. 제가 검색하면서 흥미로웠던 점이, Kingma 아저씨 논문 내용을 구현한 github 코드인데 레퍼런스로 Sohn et al. 이 달려있다거나 (Readme 수정 후 PR 날렸어요), (Sohn et al.) 논문 설명에 (Kingma et al.)의 논문 코드가 첨부되어 있는 경우들이 있더라고요. 심지어, 몇몇 논문에서는 레퍼런스를 잘못 다는 경우도 있었어요.

 

그런데, 그거 아시나요? 놀랍게도 Kingma et al. 논문의 본문에는 한 번도 Conditional Variational Auto-Encoder 혹은 CVAE라는 말이 등장하지 않습니다. 정확히 논문에서는 Conditional generative model (M2)라고 부르고 있습니다. 하지만 그 기법의 생김새를 보자면 CVAE라고 부르는 게 너무 자연스러워요. (자세한 이유 설명은 뒤에서 할게요.) 반대로 Sohn et al. 논문에서는 명확하게 CVAE 기법을 제안한다고 이야기하고 있어요. 아래의 그림은 Sohn et al. 논문의 본문인데요, 여기서 [15]에 해당하는 레퍼런스가 바로 (Kingma et al. NIPS 2014) 논문이에요.

 

Sohn et al. "Learning Structured Output Representation using Deep Conditional Generative Models" NIPS 2015 본문 캡쳐.

 

흥미롭지 않나요? 그럼에도 불구하고 누가 진짜 CVAE인가에 대해 저보고 결론을 내리라고 하신다면, 둘 다 CVAE라는 이름으로 불릴 수 있다는 겁니다. (Sohn et al., 2015) 논문의 경우 저자들이 제안 기법 이름을 CVAE라고 하였기 때문에 논란의 여지가 없고, (Kingma et al., 2014)의 경우 이미 다양한 후속 논문들에서 CVAE라는 이름으로 해당 논문을 인용하고 있어요. (더욱이 DP Kingma 아저씨가 VAE 논문을 쓴 장본인인 데다, VAE의 변형 + conditional generative model이라고 하니 conditional vae라는 이름이 꽤 자연스러우니까요)

 

Qian et al. "AutoVC: Zero-Shot Voice Style Transfer with Only Autoencoder Loss", ICML 2019.

 

이미 많은 사람들이 (Kingma et al. 2014)의 Conditional generative model을 CVAE라고 부르고 있기 때문에 누가 진짜 CVAE다를 논하는 것은 무의미한 것 같아요. 다만, 이 글을 읽으시는 분들의 경우, CVAE에 대해서 설명하는 자료를 만드시거나 논문에서 인용하실 때 레퍼런스 관리에 유의하셔야 한다는 사실을 전달하고 싶었어요. 왜냐하면, 생각보다 많은 문서들에서 이들의 레퍼런스를 잘못 달거나, 두 개의 내용을 섞어서 설명하는 경우들을 봤거든요. 이런 사소한 부분에서 글의 신뢰도가 결정되기도 하고, 대부분 그런 목적으로 글을 작성하신다면 읽는 독자들이 그것을 기반으로 배울 확률이 높기 때문에 이를 명확히 해보는 게 좋지 않을까 싶었습니다.

 

 

글을 시작하기에 앞서 말했던 주제의 결론이 벌써 나버렸네요. 하지만, 여기에서 마무리하기는 조금 아쉬우니, 각 논문의 기법이 어떻게 생겼길래 CVAE라고 이름이 붙었는지 간략히 설명해 볼게요. 아래의 설명은 VAE는 알고 있다고 가정하고 작성하겠습니다.

 

 

 

CVAE라고 불리는 각각의 논문에 대하여

 

💎 (DP Kingma et al. 2014)의 CVAE ⎯ Conditional generative model (M2)

 

(Kingma et al. 2014)에서 제안하고 있는 Conditional generative model은 VAE의 변형이라고 할 수 있습니다. VAE와 동일하게 입력 $\mathit{x}$의 log-likelihood를 maximization하는것이 목표이지만,  기존의 VAE가 입력$\mathit{x}$ 과 latent embedding $\mathit{z}$로만 표현되었던 것과 달리, Conditional generative model에서는 label 정보인 $y$가 latent embedding $\mathit{z}$를 추론할 때 사용될 뿐 아니라, $\mathit{x}$를 생성할 때도 사용된다고 가정하고 있습니다. 이를 요약하여 VAE와 비교하면 아래의 표와 같습니다.

 

	VAE	(DP Kingma et al. 2014) Conditional generative model
Inference model	$q_{\varphi }(\mathit{z}|\mathit{x})$	$q_{\varphi }(\mathit{z}|\mathit{x},y)$ $q_{\varphi }(y|\mathit{x})$
Generative model	$p_{\theta }(\mathit{x}|\mathit{z})$	$p_{\theta }(\mathit{x}|\mathit{z},y)$

 

조금 어렵게 느껴지신다면 위의 표를 다음 그림과 같이 간략하게 표현할 수 있을 것 같아요:

 

 

VAE에서 인코더가 추론 모델의 파라미터를 구성하고, 디코더가 생성 모델의 파라미터를 구성하기 때문에, CVAE는 각각 인코더와 디코더의 출력으로 라벨 정보인 $y$가 추가되는 형태라고 보시면 됩니다. 그러면 실제 생성모델 $p(\mathit{x}|\mathit{z},y)$을 통해 주어진 라벨 값에 따른 입력 데이터의 분포를 얻을 수 있습니다. 본 모델의 동작을 좀 더 자세히 설명해 주는 그림은 아래의 그림입니다. 이 그림은 제가 그린 그림은 아니고요. 이활석님의 slide share 장표에서 발췌하였습니다.

 

 

이 그림은 probabilistic graphical model은 아니고, 네트워크의 동작을 간략화해 놓은 거예요. ($h$는 레이어라고 생각하시면 될 것 같아요) 위의 그림에서 $y$에 해당하는 부분을 없애면 VAE의 동작과 같다는 것을 알 수 있습니다. 이러한 관점에서 본 기법은 label 정보인 $y$를 condition으로 하는 VAE로 볼 수 있어요. 따라서, 많은 사람들이 본 기법을 conditional variational autoencodere, 즉 CVAE로 부르고 있는 것 같습니다.

 

💎 (Sohn et al. 2015)의 CVAE

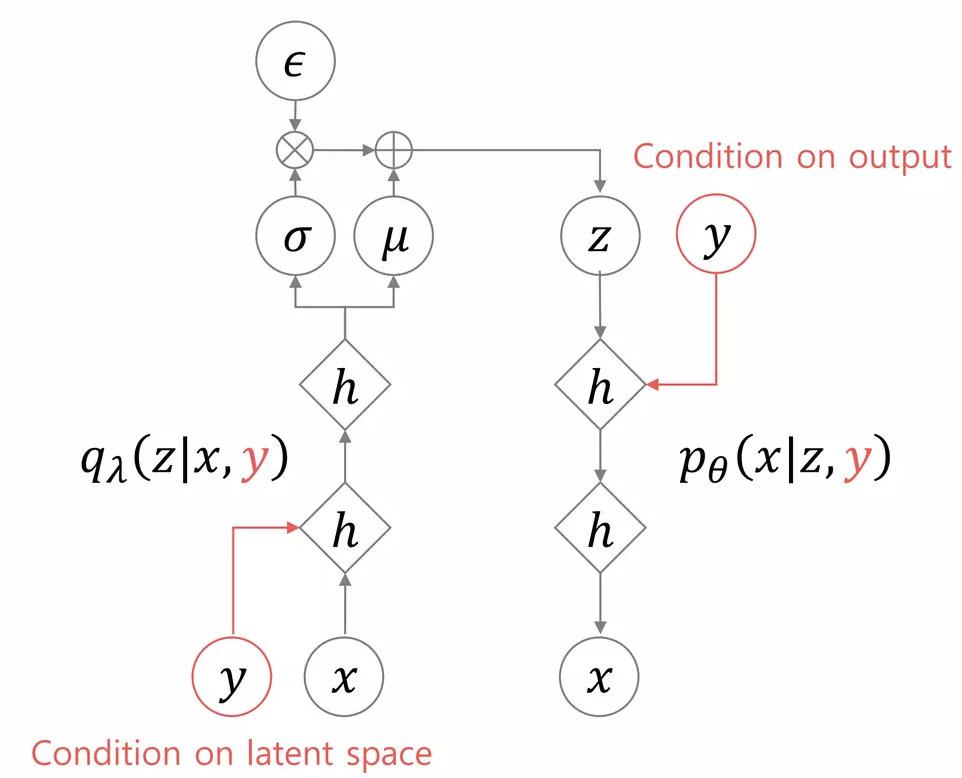
Sohn et al. 의 CVAE는 애초에 observation인 evidence $\mathit{x}$의 log-likelihood $\log p(\mathit{x})$를 maximize하는 것과 학습 목표 자체가 다릅니다. 주어진 입력 $\mathit{x}$로부터 high-dimensional output $\mathit{y}$를 추론하는 conditional distribution $p(\mathit{y}|\mathit{x})$을 찾는 것이 CVAE의 목표입니다. 참고로 여기서 $\mathit{y}$는 label이 아닙니다. 무튼 뭔지는 모르겠지만 고차원의 무언가예요.

 

 

We model the distribution of high-dimensional output space as a generative model conditioned on the input observation. (중략) The CVAE is a conditional-directed graphical model whose input observations modulate the prior on Gaussian latent variables that generate the outputs.

 

 

더 자세한 내용을 설명하기에 앞서, CVAE의 활용 예시를 먼저 보여드릴게요. 아래의 그림은 Sohn et al. 논문에 있는 실험 결과입니다. 맨 윗줄의 ground-truth 그림의 1/4에 해당하는 진한 영역이 입력 $\mathit{x}$가 되고, 연회색 부분이 출력인 $\mathit{y}$ 가 됩니다.

 

CVAE 기법은 입력 변수 $\mathit{x}$, 출력 변수 $\mathit{y}$ 그리고 은닉 변수 (latent vadriable) $\mathit{z}$로 구성됩니다. (다시 한번 강조, 여기서 $\boldsymbol{y}는 Kingma et al. 논문과 달리 라벨이 아닙니다) 이 세 개의 변수의 관계 정의를 바탕으로 CVAE 기법이 정의되는데요, 다음의 그림은 CVAE에서 세 변수 사이의 관계를 보여줍니다.

 

 

위의 그림에서 보시면 일반적인 CNN이 $\mathit{x}$로부터 $\mathit{y}$를 바로 추론하는 구조를 가질 수 있는것과 달리, CVAE의 conditional graphical model (CGM)은 latent variable인 $\mathit{z}$로 $\mathit{y}$를 설명합니다 ($p(\mathit{y}|\mathit{x},\mathit{z})$). 위의 그림에서 (b)는 generative model을 보여주고, (c)는 inference model을 보여주고, (d)는 이들을 합쳐놓은 형상을 보여줍니다. (b)의 생성모델을 살펴보면, $\mathit{y}$의 생성 모델이 단순히 $\mathit{x}$만을 가지고있는 것이 아니라, 중간에 $\mathit{z}$ 역시 condition으로 차용합니다. 따라서, (a) 그림과 다르게 $\mathit{z}$를 주입함으로서 하나의 입력 $\mathit{x}$로부터 여러 가능성 있는 출력 값을 만들어내는 multi-modality를 다룰 수 있습니다.

 

multi-modality는 one-to-many를 가능하게 해요. 이 말은 하나의 입력으로부터 여러 개의 가능성있는 출력들을 생성해낼 수 있다는 겁니다. CVAE의 이러한 특성때문에 multi-modality를 고려해야하는 분야에서 많이 차용되고있어요. (예, trajectory prediction 지금까지 걸어온 보행자의 trajectory가 있다고 했을때, 하나의 예측값만을 반환하는 것은 문제가 있습니다. 여러개의 가능성을 보여줄 필요가 있죠.)

 

이러한 생성 모델을 갖는 CVAE는 어떻게 학습될까요? 다시 처음으로 돌아가서, CVAE의 목적은 conditional log-likelihood maximization입니다. 다시 말해서 $\log p(\mathit{y}|\mathit{x})$를 최대화하는 것인데, VAE에서와 마찬가지로 이를 바로 maximization하지 못하고 해당 값의 lower bound를 maximization하는 형태로 학습이 이루어집니다. 그리고 conditional log-likelihood의 lower bound는 다음과 같이 유도할 수 있습니다. (논문의 본문과 조금 다른 형태로 유도하였습니다)

 

$$ \begin{align*}

&\log p_{\theta}(\boldsymbol{y}\vert\boldsymbol{x}) \

& = \log \int_z p(\boldsymbol{y},\boldsymbol{z}\vert\boldsymbol{z})\ & = \log \int_z \frac{p(\boldsymbol{y}, \boldsymbol{z}\vert\boldsymbol{x})}{q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})} q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{z}\ & \geq \int_z q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})\log\frac{p(\boldsymbol{y}, \boldsymbol{z}\vert\boldsymbol{x})}{q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})} dz \&=\int_z q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})\log\frac{p(\boldsymbol{y}\vert \boldsymbol{z},\boldsymbol{x})p(\boldsymbol{z}\vert\boldsymbol{x})}{q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})} dz \ &=-\text{KL}(q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})\vert\vert p(\boldsymbol{z}\vert\boldsymbol{x}))+\mathbb{E}_{q(\boldsymbol{z}\vert\boldsymbol{x},\boldsymbol{y})}[\log p(\boldsymbol{y}\vert\boldsymbol{x},\boldsymbol{z})]\end{align*}$$

 

CVAE의 conditional log-likelihood의 lower bound 도 VAE와 유사하게 regularizer와 expected reconstruction term으로 구성됩니다. 여기서 뒤에 있는 항의 연산을 위해 VAE의 Stochastic Gradient Variational Bayes (SGVB)를 사용해서 reparameterization trick으로 연산됩니다.

 

(+) SGVB 연산 시 Monte-Carlo (MC) Sampling을 사용하는 것이 일반적인데, 본 논문에서는 Impotance Sampling도 사용하였습니다. 자세한 내용은 논문을 참조하시거나, 추 후 Importance Sampling과 관련한 글을 쓸 때 소개드려볼게요.

 

그러면 구체적으로 conditional log-likelihood의 maximization은 어떤 네트워크에 대해서 이루어질까요? graphical model에 나타난 $q(\mathit{z}|\mathit{x},\mathit{y})$, $p(\mathit{z}|\mathit{x})$,  그리고$p(\mathit{y}|\mathit{x},\mathit{z})$ 를 표현하는 네트워크로 구성됩니다. 논문에서 생성 모델의 파라미터들을 $\theta$로, 추론 모델의 파라미터를 $\varphi$로 나타내고 있지만, 엄밀한 의미에서 generative model에 사용되는 네트워크는 두 개인 셈입니다.

 

이렇게 보니, (D.P. Kingma 2014)의 논문과 목적부터 그 형태가 굉장히 다르다는 것을 아시겠나요? 좀 더 자세히 설명하려면 본 글의 취지와는 멀어질 것 같으니, 더 자세한 내용은 필요하다면 나중에 다뤄보겠습니다. 그러면 이제 마무리, CVAE 논문은 왜 CVAE라고 이름을 붙였을까요? VAE의 변형이라고 하기에는 목적함수부터 모양이 달라서 헷갈리는데 말이죠. 저자들도 이에 대해서 논문에서 언급하고 있습니다. 

 

 

conditional distribution의 분포를 variational inference 방식으로 추정한다는 점에서, 그리고 그 추정 과정에서 SGVB를 사용한다는 점에서 VAE의 변형으로 볼 수 있고, conditional likelihood에 대한 VAE 형태를 적용하고 있으므로 CVAE라고 이름 붙인 것 같습니다.

 

마무리,

 

글의 소재가 생각났을 때, 꽤 도움이 될만한 소재라고 생각했습니다. 제가 찾아보는 입장에서도 혼란스러운 콘텐츠가 많았고, 레퍼런스가 엉켜있다는 느낌을 많이 받았거든요. 그러면서도 한편으로는 '내가 지금 잘못 생각하고 있는 건 아닐까?'라는 생각도 들었어요. 그래서 누군가는 잘못된 오개념을 맞다고 생각할 수도 있겠다는 생각이 들어 글을 쓰게 되었습니다. 두서없이 글을 쓰다 보니, 오류가 있을 수 있어요. 발견하신다면 언제든지 알려주시면 큰 도움이 될 것 같습니다.

 

 

여담.

저는 요즘 전문적인 글을 쉽게 설명할 수 있는 능력을 갖추자는 생각을 갖고 있어요. (그래서 블로그를 시작했습니다) 진짜 고수들은 엄청 어려운 내용도 진짜 쉽게 설명하잖아요. 저는 아직 엄청 어려운 내용을 엄청 어렵게 설명하는 것도 미숙하지만, 최대한 직관이나 이해를 전달할 수 있는 관점에서 글을 적어보는 연습을 하고 있어요. 다음에는 조금 더 유익한 글을 가지고 와볼게요.

 

이 글을 작성하던 중에 드래프트를 한번 날렸어요. 임시저장을 해가면서 쓰고 있었는데, 임시저장한 드래프트가 지워진 채로 자동저장이 돼버려서.... 💨 솔직히 말하면 다시 쓰기 정말 싫었어요. 하지만, 이 글이 누군가에게는 도움이 될 수도 있지 않을까라는 생각이 들어서 꾸역꾸역 처음부터 다시 썼습니다. 심지어 그림도 다 다시 그렸어요...😭 (저장할 필요 없을 거라 확신했던 과거의 나)

 

원래 버전에서는 좀 더 말투도 친절하고, 친근했는데, 두 번째 쓰다 보니 좀 딱딱해졌네요. 티스토리 글쓰기 플랫폼에 조금 화가 났나 봅니다. 그래도 조금은 도움이 되는 글이었길 바랍니다.

 

 

 

 

썸네일용 사진

글 읽느라 너무 고생하셨으니,

귀여운 거 보고 가세요

 

 

 

끝 ◼︎